On the ‘quindecile’ aspect

On the historical and modern concepts of the ‘quindecile’ aspect
– Written by Philip Graves, January 3rd-4th, 2010
– Updated with footnotes, January 7th 2016 and January 20th 2016;
– Transcription of Ring’s German slightly corrected, January 21st 2016

Note: the main text of this article was originally part of a vigorous debate with a fellow Skyscript forum-member, “Atlantean”. It is therefore broken up into segments based on my responses to his arguments there. His original comments are not reproduced here but can probably still be found archived at Skyscript.

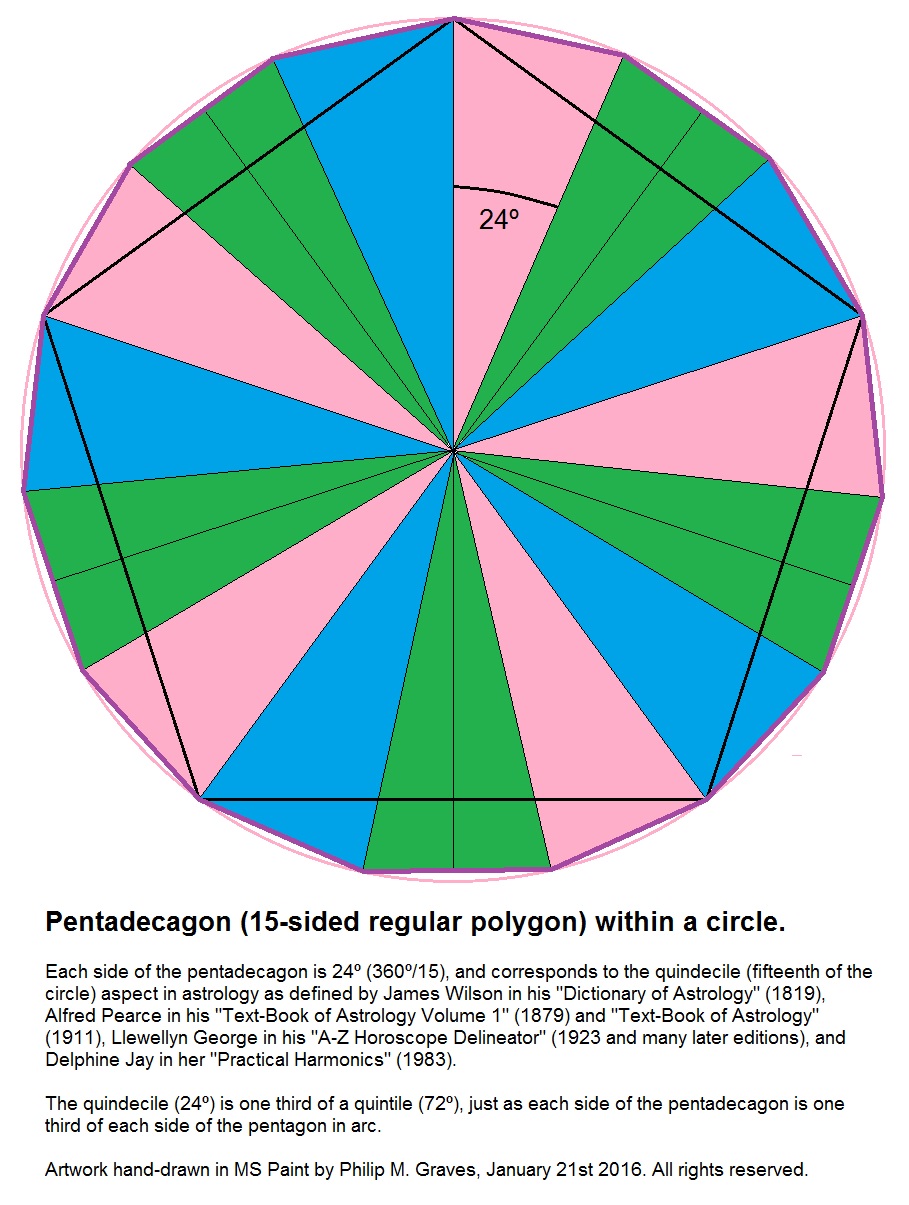
James Wilson, writing in the first edition of his ‘Dictionary of Astrology’ (1819), p. 99, under ‘Familiarities’, expressly attributes the invention of the quindecile to Kepler (p. 99) and goes on to define it (p. 100) thus:

“The Quindecile, a distance of 24º, is the circle divided by 15.”

Therefore it is my firm belief that the term ‘quindecile’, having been already well-established under this, its logical definition, within at least one major work within the English-language astrological literature by as long ago as 1819, has been misappropriated and misused by Ricki Reeves and whoever might have taught her.

Considering the possible astrological influence of the 165 degree aspect is perfectly legitimate of course, but giving it a name that not only does not conform to the conventional basis on which aspect names are generally given, but also already exists in perfect conformity to that conventional basis in the established literature to describe another aspect altogether, was a recipe for muddying the waters of astrological nomenclature.

I think it is a positive mistake to continue to call either the 15 degree aspect or the 165 degree aspect a ‘quindecile’. It is tantamount to inventing a 174 degree aspect and calling it a ‘sextile’, or inventing a 177 degree aspect and calling it a ‘trine’. Such a practice would outrage any astrologer. So should the misuse of ‘quindecile’.

*****

[In response to “Atlantean”‘s observation that a Google search finds a greater prevalence of the use of the term ‘quindecile’ in reference to the 165º aspect than to the 24º aspect, and that James Wilson is a ‘virtual unknown’ as compared with Thomas Ring, credited by “Atlantean” with the initiation of the ‘present usage’ of the term ‘quindecile’:]

I beg to differ regarding James Wilson, who was one of the major astrological writers of the early 19th century, and whose Dictionary of Astrology has gone through several printings, both in the UK and in the USA. It is not an obscure work at all in the history of astrology, but rather a very famous one.

I disagree that counting the number of google search results for a particular term is a relevant way to resolve its meaning. The vast majority of those results for the term quindecile (in English) are a direct result of the publication of Ricki Reeves’ book on the single topic of the 165 degree aspect early in the days of the Internet. Of course a whole book written on that one theme has attracted a lot of discussion, whereas in the context of Wilson’s dictionary, the quindecile was merely one of several aspects he listed and attributed to invention by Kepler.

This does not make the historical case any less important in my opinion, on grounds of both nomenclature convention and the actual historical reference in a major work naming the 24 degree aspect as the quindecile.

Nor should there be lacking a practical case for the consideration of the 24 degree aspect from any adherent of harmonic theory. The division of the circle by (3*5) is arguably as natural a consideration as the division of the circle by (2*5) or (2*3).

In contrast, the 15 degree aspect and its 75 degree, 105 degree and 165 degree multiples stem from the division of the circle by (2*2*2*3). This is arguably a more intricate division of the circle than (3*5). I think the mere fact that analysis of the 165 degree aspect has lately perhaps been more commonplace than that of the 24 degree aspect says nothing for their relative degree of theoretical and practical usefulness in astrology. Fashions come and go.

I wholly disagree that my analogy with the sextile is absurd. The main reason that more astrologers are not outraged by the misappropriation of the term quindecile to mean something different, in my opinion, is that they have not stopped to consider how the naming pattern works. Even if we are to presume that almost no astrologer today is familiar with Wilson’s dictionary, the aspect names follow a consistent pattern based on the number by which the circle has been divided, and within this pattern the term ‘quindecile’ clearly denotes the division of the circle by 15 regardless of whether or not references to this in the historical literature are familiar to most of today’s astrologers.

*****

I just thought I should fill in on the printing history of James Wilson’s Complete Dictionary of Astrology for the record:

1. First published 1819 by William Hughes, Islington Green, London. 2. Revised and corrected edition published 1820 (though undated) by William Hughes 3. First American edition published 1885 by Rolfe & Co., Boston, Mass., 1885 4. Reprinted by Samuel Weiser 1969 5. Second Weiser printing 1970 6. Third Weiser printing (but sold as second) 1971 7. Health Research reprint (comb-bound) 1971 8. Fourth Weiser printing (sold as third) 1974 9. Fifth Weiser printing (sold as fourth) 1978 10. Kessinger Publishing (print-on-demand) reprint 2003 11. Astrology Classics reprint 2006

By my reckoning that makes it a common book with many thousands of copies in print. However, it is interesting to note that Thomas Ring’s work was mostly published in the 1950s and 1960s, some 70 years since the previous impression of Wilson’s book. He may therefore quite plausibly have been unaware of it, if indeed he was the one who adopted the term ‘quindecile’ with a completely new meaning.

Wilson is also noted historically for having made one of the earliest printed translations in English of Ptolemy’s Tetrabiblos (or at least the Proclus paraphrase thereof). His translation came after that of Whalley but predated that of Ashmand. Unlike his Dictionary of Astrology, however, his translation of Ptolemy is very scarce.

I am raising issues of what I believe to be principles of systematic coherence as well as history.

I would really appreciate a reference to Ring’s original use of the term quindecile since this is an important piece of astrological history from where I am looking. I do not have all his books, but so far am leafing through Astrologische Menschenkunde Book 1: Kräfte und Kräftebeziehungen (first printing 1956). In the section on Aspects, Ring mentions the 15 degree, 75 degree, 105 degree and 165 degree aspects together on p. 250. I quote:

“Schließlich kann für Beurteilungen der Feinstruktur über die Zwölfteilung hinausgegangen werden zum Vierundzwanzigeck, mit den Winkel von 15º, 75º, 105º und 165º.”

Then on p. 278 he continues:

“Wird die zwölfstufige Ordnung durch weitere Aufspaltung verdoppelt im Vierundwanzigeck, so entsteht eine regelmäßige Figur mit 15º-Aspekten, worin neben sämtlichen Aspekten der Zwölferordnung die schon dargestellten [Quadrat] und [Anderthalbquadrat] mit umfaßt sind. Als neu sondern sich 15º, 75º, 105º, 165º aus…. Als besonders eigenartig sei nur der 165º-Aspekt herausgehoben, charakterisierbar als feiner, trennender Schnitt, bei analogen sonstigen Anzeichen deutbar als Beitrag zu schicksalhaften Trennungen, seelischen Amputationen usw. Aspekte dieser Ordnung gelten lediglich als Bestätigung von Tendenzen, die in normalen Aspekten schon angezeigt sind.”

This is all very interesting as an introductory exposition to Ring’s approach to these aspects and in particular his interpretative slant on the 165 degree aspect, but I am still looking for evidence that he coined the term quindecile. He shows clear and strong awareness in these extracts of the sourcing of the 165 degree aspect in the division of the circle by 24, repeatedly using the word ‘Vierundzwanzigeck’ to describe them collectively.

I would have to ask why on this basis Ring himself would have sought to use the term ‘quindecile’ rather than ‘quartvigintile’ (or similar), if he were to write in English. Did he in fact use the label ‘quindecile’ (or the direct German equivalent) in some of his writings, or might this possibly be misunderstanding or free licence taken by the later translators and popularisers of his ideas in English? I’m happy to reserve judgement on this pending further relevant references.

PS: In the introduction to Ricki Reeves’ book, I note that Noel Tyl claims personal responsibility for coining the term ‘quindecile’, to be pronounced in Italian, for reasons of sonorous aesthetics rather than historical conformity. Therefore I at this stage have serious doubts that Ring ever used the term or would in any way have sanctioned it.

Kudos to Noel Tyl for taking Thomas Ring’s observations and making a serious study out of them, and I have a lot of personal respect for the man as an inspiring astrological teacher who has committed a great deal of his life to his vocation. Yet I still don’t personally believe that his case for renaming a 24th harmonic aspect ‘the quindecile’ (if indeed the use of the word in this way is, as he claims, of his own coining) is a strong one.

From what I can see so far, Ring was true to the history of aspect nomenclature in using the word ‘Vierundzwanzigeck’.

In ‘Astrology of the Famed’ (1996), published five years before the Ricki Reeves book, Tyl states that the 165 degree aspect is called the quindecile. He refers to Leonardo da Vinci’s birth data as it appears on the pull-out final leaf of Ring Volume I (1956 – the same volume from which I quoted above) but refers the reader to Ring’s apparently later book ‘Genius und Dämon’ (1980) for Ring’s analysis that inspired Tyl himself to investigate the 165 degree aspect.

Clearly Ring was already advocating the importance of the 165 degree aspect in 1956. Nonetheless, I want to investigate this further so I plan to order a copy of ‘Genius und Dämon’ shortly. There are quite a few on the used book marketplace.

So far the earliest reference I can find to the use of the term quindecile to mean 165 degrees is Tyl (1996).

*****

By way of providing evidence that James Wilson is far from being the only major astrological writer who has drawn attention to the 15th harmonic aspect of 24 degrees, which Wilson called the quindecile, I wish to point out that John Addey devotes almost three pages of his extremely well-known modern work ‘Harmonics in Astrology’ (1976) to expressly speaking of the importance of the 24 degree aspect in astrology. See pp. 172-174. I shall quote just the first paragraph but believe this piece of recent history penned by a widely respected leader in modern astrological research in the mid-late 20th century undermines any claim to the 165 degree aspect being regarded as ‘the useful quindecile’ or similar in modern practice.

“One very important derivative of the quintile series which is almost entirely ignored, as a rule, is the third sub-harmonic of the quintile, which gives us the aspect of 24º and its multiples. This is the fifteenth harmonic, the third of the fifth or the fifth of the third. Figure 60 shows the aspect angles involved. It will be seen that this series includes the angles of 72º, 120º and 144º with which we are familiar but also the angles 24º, 48º, 96º and 168º which are not customarily used or understood but which are certainly important and can now be given quite a definite meaning in the horoscope. “

Nomenclature is not an issue here. Addey does not go into names for the aspects much at all, preferring to refer to them in descriptive long-hand in relation to their place in harmonic theory. Otherwise he is only concerned with studying them in practice.

*****

I have just been refreshing my memory of the work of David Hamblin and Delphine Jay on the harmonics. They both treat of the fifteenth harmonic and accord it significance. Whereas Hamblin, like Addey before him, is content to give a purely narrative description of each aspect in terms of harmonic theory (e.g. the ‘fifth harmonic trine’), Jay expressly names each aspect.

The source for Jay is her book ‘Practical Harmonics’ published by the American Federation of Astrologers, Inc., Tempe, Arizona, 1983.

See page 10, where she expressly names the 24º aspect the quindecile, just like Wilson 164 years before her.

Therefore my impression is that Noel Tyl (1996) and (following in his foosteps) Ricki Reeves (2001), in adopting the name ‘quindecile’ for the 165º aspect, have overridden the precedent set not only by James Wilson in 1819 but also Delphine Jay as recently as 1983. This is an unfortunate state of affairs in my opinion that can only serve to cause confusion.

In short I simply do not accept that ‘the change has been made; it’s no use crying over spilt milk’. It currently appears to me from the available evidence highly probable that the ‘change’ (which could equally be viewed as an unsatisfactory duplication of names for different concepts rather than a replacement) dates back only to 1996, and not to the work of Thomas Ring; while as recently as 1983 the term quindecile was still being used in print to refer to the 15th harmonic (24º) series of aspects, and all three of the major interpretative English-language books on harmonic theory of the 1970s and 1980s have expressly drawn attention to the importance of the 15th harmonic aspects in astrological interpretation. What I see as being more the historical reality here rather than a ‘change’ is that two concepts that have concurrently seen a large amount of use in modern astrology albeit from the points of view of different schools of thought have ended up being given the same name as each other, though the 15th harmonic aspect got the name first and had had it for the best part of two centuries before the 24th harmonic aspect was given it. This does not logically mean that the Tyl-defined (24th harmonic) quindecile has rendered the Wilson / Jay-defined (15th harmonic) quindecile invalid or superseded in astrological use. That such an impression may have been obtained, alas, is part of the inherent drawback of the duplication of names. So long as there are advocates of harmonic theory, the 15th harmonic aspect will be used, and the quindecile is the logical name for it.

I don’t accept that the application of harmonic theory in modern astrological practice is dead or has died since 1983 either. These ideas were certainly still very current in the 1990s, and Addey’s book for one has continued to be reprinted in the 2000s. The quindecile as used by all the adherents of this school needs a name too, and already has one that perfectly describes what it is, consistently with the traditional principles of aspect terminology, so let’s keep using it.

If you are looking from this issue as a past student of Noel Tyl, then of course that will be your primary source of reference. But while I admire him very much in many ways, Noel Tyl is not representative of the only major current in modern astrological thinking with regard to the harmonics and minor aspects.

I do think however that there may be a case for adopting a term like ‘Tyl / Reeves quindecile’ to distinguish it from the traditional quindecile, among those who have got used to that name and do not wish it to be changed more radically to something more in tune with what Thomas Ring suggested in German (to judge by the extracts from his 1956 work I quoted directly in an earlier message), which would be in accordance with the tradition: something along the lines of quartvigintile for the 24th harmonic series that includes the 165º aspect – or in terms of harmonic theory, it has been described by some of the English authors I mentioned above as the 4th harmonic sextile.

*****

1. Another important 20th century source predating Delphine Jay by several decades that addresses the quindecile is:

Llewellyn George ‘A to Z Horoscope Maker and Delineator’*

In the section headed ‘Part I: the Natal Chart’ (p. 93 in the 7th edition, 1939; p. 85 in the 4th edition, 1928; pp. 91-3 in the 29th edition, 1972), George writes under ‘Minor Aspects’:

“Quindecile – 24 degrees apart, slightly good, has an orb of 2 degrees”

In the section headed ‘Part V: Additional Studies’, George further describes the quindecile thus (7th edition, 1939: p. 720; stated 3rd edition [but 2nd?], 1913: p. 353; 3rd edition, 1923: p. 409; 4th edition, 1928: p. 647; 29th edition, 1973: p. 784):

“Another of Kepler’s minor aspects; 24 degrees, slightly good”.

Llewellyn George’s cited work above is probably one of the best-selling astrological text-books of the 20th century, having been through about thirty printings between 1910 and the late 1970s, prior to being reworked in a shorter format from the 1980s onwards. I believe this demonstrates that even if Wilson’s Dictionary of Astrology was hard to obtain for many in the early-to-mid 20th century after the 1885 printing fell out of print and before the 1969 impression was produced, the traditional definition of the quindecile was still in common currency thanks to the oft-reprinted textbook of Llewellyn George, at least in the United States of America.

*1913 and 1923 editions are called ‘A to Z Horoscope Delineator’; I do not have the 1910 first edition but this had the same name too

2. Further, the earlier continuity of the tradition at least on the level of nomenclature through the late 19th century in England is demonstrated in:

Alfred Pearce ‘Text Book of Astrology’ Volume 1 – Cousins & Co., Covent Garden, London, 1879

I quote from p. 39: ^#

“There are other aspects, viz., the vigintile (18º), the quindecile (24º), the decile (36º), the quintile (72º), the tredecile (108º), the biquintile (144º), and the quincunx (150º). All these aspects were invented by Kepler, and their influence is undeniable, with the exception of the vigintile, quindecile, and the tredecile, which require confirmation.”

So Pearce, who was quite a traditionalist, was perhaps a natural sceptic towards novel ideas but nonetheless open-minded, whereas Llewellyn George seems for his part to have been more openly sold on the utility of the quindecile in interpretation.

^# NB: In the 2nd edition of Pearce, published by Mackie & Co., Ld., Warrington and Fleet Street, London, and by Simpkin, Marshall, Hamilton, Kent & Co. Ld., 1911; also reprinted much later by the National Astrological Library, 1950s, and by the American Federation of Astrologers, 1970 and 2006, this quotation appears instead on pp. 30-1

3. I do not have all Kepler’s works by any means, but am trying to find the possible source for the claim in James Wilson, Alfred Pearce and Llewellyn George that Kepler invented the quindecile (24º) aspect. In:

Johannes Kepler ‘The Harmony of the World’, translated by E. J. Aiton, A. M. Duncan and J. V. Field, American Philosophical Society, 1997:

Book IV, Proposition XV, pp. 347-8:

Kepler groups together the 15th and 20th harmonic astrological aspects as being, in the translators’ words:

“configurations which are on the borderline between influential and non-influential, namely the arc of 24º from the pentekaidecagon (fifteen-sided figure), and 18º from the icosagon”.

Kepler expressly includes the multiples of the 15th harmonic series, 48º, 96º and 168º, in his description (p. 348). He also includes two others in error, as the editors note in their footnote.

I do not have the presumed German original (unless it was Latin – I confess I do not know), but it seems clear that if the reference made was to a figure that the translators have called a pentekaidecagon, Wilson was not being unreasonable to transpose this in astrological lingo to quindecile, if indeed he is the earliest source of the English language version, which remains to be proven.

*****

[In response to “Atlantean”‘s objection that ‘the 24th division would seem to be much more likely to be important’ (than the 15th division of the 360º circle, as a basis for the derivation of astrological aspects):]

Interesting argument, but I’m afraid I don’t agree!

On this basis, it could be argued that the 120th harmonic aspects (e.g. 3 degrees, 177 degrees) would be more important than either the 24th harmonic ones or the 15th harmonic ones, since they would include not only the conjunction, semi-sextile 10/120ths, semi-square 15/120ths, sextile 20/120ths, square 30/120ths, trine 40/120ths, sesquiquadrate 45/120ths, quincunx 50/120ths, opposition 60/120ths, and Tyl / Reeves ‘quindecile’ 55/120ths… but also the quintile 24/120ths, bi-quintile 48/120ths, decile 12/120ths, tridecile (a.k.a. sesquiquintile) 36/120ths, quindecile 8/120ths, bi-quindecile* 16/120ths, quadri-quindecile* 32/120ths, and septi-quindecile* 56/120ths, not forgetting the vigintile 6/120ths and its multiples….

This argument fails in my opinion, since the greater the circle division factor, the more major and minor aspects will fit into its pattern, but you are also introducing aspects that are more and more absurdly minor for each further division, and it should be the importance of these base aspects which cannot be derived from a simpler division of the circle that is the standard by which to judge the circle divisor, and not the number of multiples of these aspects that can equally be obtained readily from a simpler division of the circle.

NB: My calculations of fractions above are pure mental arithmetic on-the-fly so if I made any mistakes please forgive them – I’d be glad to put them right.

* for the sake of a working terminology that is more or less consistent with tradition – not definitive terms

*****

[In further response to “Atlantean”:]

Considering that Noel Tyl in Astrology of the Famed (1996) cites the delineation of Leonardo’s horoscope from a book by Ring that was published in 1980, I personally feel that to say the aspect was lost then ‘rediscovered’ is stretching the truth a little. Ring’s work has been popular in Germany continuously. What Tyl did was to discover it for himself, then conduct his own research, and re-present it to the English speaking marketplace. It had never been ‘lost’.

This reminds me a bit of the hyperbole surrounding the supposed ‘rediscovery’ of the ‘Law of Attraction’ by Jerry and Esther Hicks and Rhonda Byrne, the latter marketing it as ‘The Secret’. These ideas have been out there all along in books from the early 20th century. Some people just have a keen eye for marketing in my humble opinion.

I read the history section of Ricki Reeves’ book you refer to late last night, hence my comments overnight regarding Tyl’s sources in ‘Astrology of the Famed’ to which Reeves refers.

I still don’t agree with your reasoning for the importance of the 24th harmonic, sorry to say. The only base aspects in the 24th harmonic that cannot be derived from simpler divisions of the circle than (2*2*2*3) are 15 degrees, 75 degrees, 105 degrees and 165 degrees. These and these alone are the aspects by which this division should be judged. The same argument you place for the 120th harmonic, that these might be ‘nonsense aspects’, could equally be applied here and for exactly the same reasons. The multiples of the same base aspect that can be derived more simply are completely immaterial in assessing the base aspect per se and its multiples that can only be derived from a minimum of the circle division factor that was applied (in this case 24) to obtain it.

To get the 45 degree and 135 degree aspects you do not need 2*2*2*3. You only need 2*2*2. Similarly, to get 30 degrees and 150 degrees you do not need 2*2*2*3. You only need 2*2*3.

For every additional divisor from the whole circle, an aspect becomes naturally more minor by its nature. Aspects derived from 2*2*2*3 will be more minor than those derived from 2*2*3 and those derived from 2*2*2.

In turn, those derived from 2*2*3 will be more minor than those derived from 2*2 and those derived from 2*3, and so on.

In the case of the traditional quindecile, the circle division by 3*5 is a lot simpler mathematically than that by 2*2*2*3. To demonstrate that the 24th harmonic aspects such as 15 degrees and 165 degrees are inherently more major than the 15th harmonic aspects, you are going to have to argue, in my opinion, that the division of the circle by 2*2*2 is a simpler, more natural operation than its division by 5, since both harmonics have in common a division by 3, and we can therefore factor the 3 out when comparing them. So if you believe that the quintile and biquintile are less important in astrological interpretation than the semisquare and sesquiquadrate, then I feel your argument at least becomes consistent according to the principles of how aspects are derived and how their power diminishes as they become more minor with additional divisors applied to the full 360º circle.

Kepler did not believe that the quintile and biquintile were less important than the semisquare and sesquiquare. He believed the quindecile (24º) series was of borderline influence (as per my citation above) and apparently (based on the same source) disregarded the quartvigintile (15º) altogether.

Before Ring (1956) I have found no reference to the use of the 15º aspect in astrology, unlike the several references to that of the 24º aspect. This no doubt in part because Kepler mentioned the latter but not the former.

This brings us into the later 20th century and the harmonic astrologers. Addey, Hamblin and Jay all advocate the importance of the 24º series. At least two of them also give some importance to the 15º series. They are not limited by the limitations imposed by Kepler, since they have taken harmonic theory to a new level of enquiry. Why can we not follow their example and accept both the 24º and 15º series as being of potential importance and study them both with equally open mind?

This brings me back to the whole point of my dissatisfaction with the appropriation of the term quindecile to have a new meaning. It is creating an artificial conflict between two different but theoretically comparably valid series of aspects. There should be no such conflict. Each should be free to be studied. But by giving one of them the name the other already had, Noel Tyl has generated in people’s minds the idea that one or the other series of aspects must be cast aside and regarded as relatively insignificant. This need not be the case.

*****

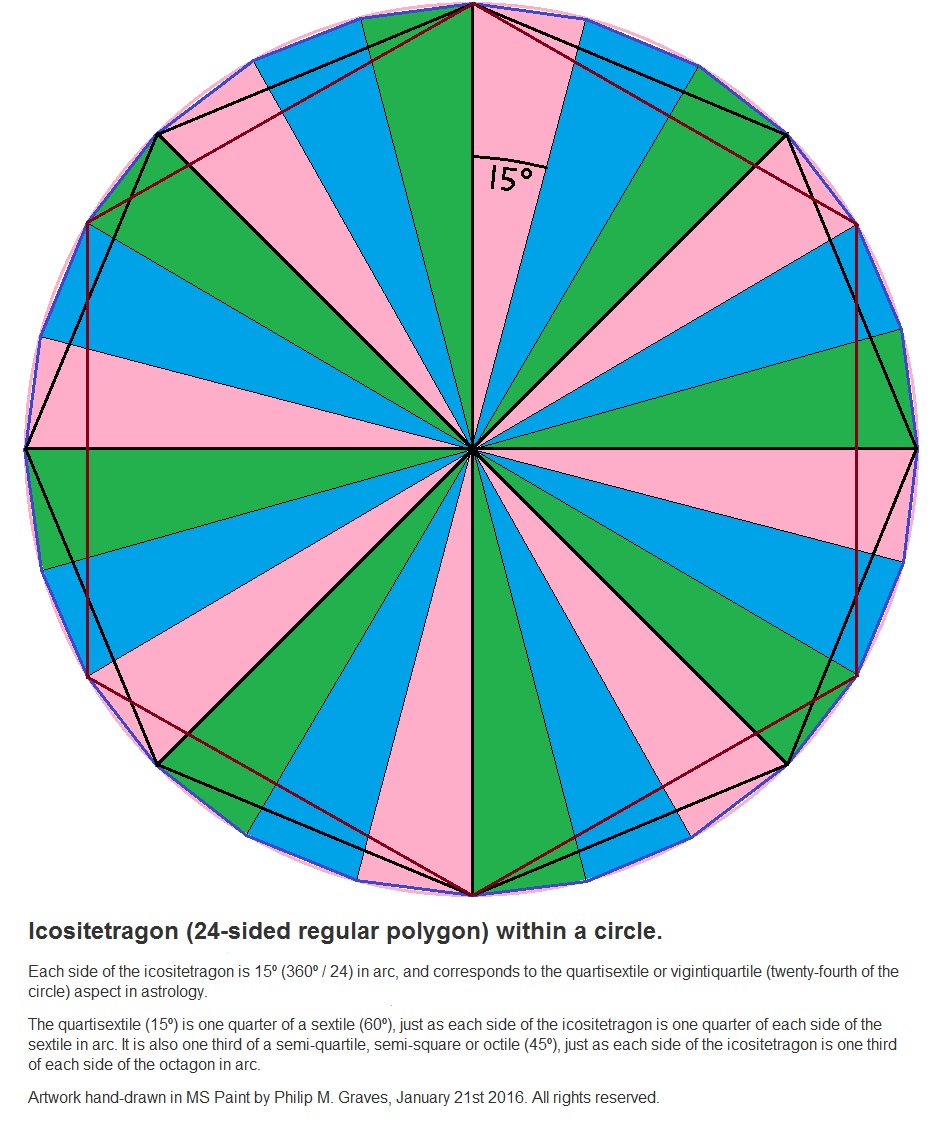
Update, January 7th 2016; revised January 21st, 2016

Following extensive discussions with my esteemed astrologer friend Michelle Young late in 2015, we jointly proposed to the astrological community the name ‘undecaquartisextile’ for the 165 degree aspect. This term not only describes eleven times one twenty-fourth of the circle of the celestial ecliptic, but demonstrates an explication of how a twenty-fourth of the circle is derived from simpler circle division factors. A twenty-fourth of the circle (15º) is of course a quarter (quarti-) of a sextile (60º). Since we already have ‘semi-sextile’ to denote half a sextile (30º), and the old term ‘quartile’ to denote a quarter of the circle (90º), why not combine them to indicate a quarter of a sixth? It seems an elegant and clear solution to the naming problem.

My equally esteemed astrologer friend Robert Wilkinson, who has been investigating harmonic aspects for more than forty years, has informed me that he has long used the Germanic “elftile” instead of “undecile” to refer to the eleventh harmonic aspect series, finding this to result in much neater and clearer names for the multiples of the eleventh harmonic; but he is equivocal about what prefix to use to denote the multiplication of other harmonic aspects by eleven. Coincidentally, I had independently proposed instead of ‘undeca-‘ as a prefix to denote ’11 times’ the appellation ‘elva-‘ in an extensive article of mine on the theory of harmonic aspect orbs submitted pseudonymously to the Astrological Association of Great Britain in the late summer of 1996 (although not ultimately published). The German for ‘eleven’ is ‘elf’, and the Swedish for ‘eleven’ is ‘elva’.

Since however most of the terms used to denote the mathematical bases for aspect names are of Latin origins, and thus we have “quintile” from “quinque” (Latin for ‘five’); “septile” from “septem” (Latin for ‘seven’), and “novile” from “novem” (Latin for ‘nine’), my personal feeling is that “undecile” from “undecim” (Latin for ‘eleven’) is in keeping with precedent and tradition for the eleventh harmonic base aspect, even though it is relatively unwieldy. Thus, it is certainly acceptable, though Robert’s long-established practice of using “elftile” has major cosmetic merits over it.

This observation does not by itself resolve the issue of how to denote multiplication of other harmonic base aspects by eleven, as for instance in the case under discussion in this article of the 165º aspect (being eleven times one twenty-fourth). But it points to “undeca-” as a compatible and logical prefix that should be readily comprehensible. For that reason, this is what Michelle Young and I jointly advocate for the time being. Thus ‘undeca-quartisextile’. But ‘elf[t]a-quartisextile’ or even ‘elva-quartisextile’ would equally well do. [The hyphens are included there just for clarity’s sake, and are essentially unnecessary.]

*****

Further update, January 20th 2016:

In response to the observation made by an astrologer friend that the late Robert Blaschke adopted the term “contra-quindecile” to denote 165º, I had the following to say in another forum today:

With all respect to the late Robert Blaschke (bless his soul), the problem I have with the name “contraquindecile” is exactly the same as the one I have with “quindecile”, which is that it does not accurately describe the mathematical derivation of the geometrical aspect.

Of course we have the contraparallel and contra-antiscion as precedents for the use of “contra-” in aspect nomenclature.

But for “contraquindecile” to be valid on this basis as a term for the aspect of 165º, it would have to serve the equivalent function to the quindecile that the contra-antiscion serves to the antiscion or the contra-parallel to the parallel.

Unfortunately, it doesn’t.

Since the term quindecile, according to the tradition of aspect names, denotes the division of the 360º circle by 15, to give 24º, if there were such a thing as a contra-quindecile it would have to be (180-24) 156º.

Since the 15º aspect is produced by the division of the circle by 24, “quindecile” is not a valid name for it in the first place, just as “sextile” is not a valid name for an aspect of six degrees, “quintile” is not a valid name for an aspect of five degrees, and “decile” is not a valid name for an aspect of ten degrees.

There are differing views on what would be an appropriate name for the 15º aspect, but it must express the circle division factor used to derive it in some way or other. This limits the range of possibilities.

Michelle and I discussed this at length a few months ago.

We could call it a demi-semi-sextile (half a semi-sextile), a vigintiquartile (one twenty-fourth), or a quarti-sextile (a quarter of a sextile – i.e. a fourth of a sixth, which is a twenty-fourth).

For the reason that it most clearly elucidates the derivation of 15º from 360º, we preferred the latter of these three possibilities.

So if you want to use Robert Blaschke’s suggestion of contra-, then you could potentially call 165º a contra-quartisextile, a contra-vigintiquartile, or a contra-demi-semi-sextile.

However, on analysis there is no precedent for the use of “contra-” in aspect nomenclature for aspects that are geometrically derived. It has only been used for ones that relate to antiscia and parallels. It would therefore introduce unnecessary confusion in my view to start using it for geometrical aspects.

If we start calling 165º a contra-quartisextile, then we could equally start calling a trine a contra-sextile (180º-60º), a sextile a contra-trine (180º-120º), or a square a contra-quartile (180º-90º) (at the same time as it is a quartile).

A tridecile (108º) could be called a contra-quintile (180º-72º). But I think “tridecile” describes it more clearly because it’s three times a decile.

A biquintile (144º) could be called a contra-decile (180º-36º). But I think “biquintile” describes it more clearly beacuse it’s two times a quintile.

For the same reasons, I think calling 165º a contra-quartisextile (or similar) is unnecessarily complicated and confusing, when undeca-quartisextile directly describes its derivation from 11 times the twenty-fourth of the circle.